Концепция тензора была создана в 1900 году двумя итальянскими математиками — Туллио Леви-Чивита и Грегорио Риччи-Курбастро, и, как это обычно бывает, основывалась на работе других математиков. Страница в Википедии о тензорах начинается так:
Звучит непросто для тех, кто не разбирается в математике!
К счастью, на практике намного проще понять, что такое тензор и как он используется в науке о данных.
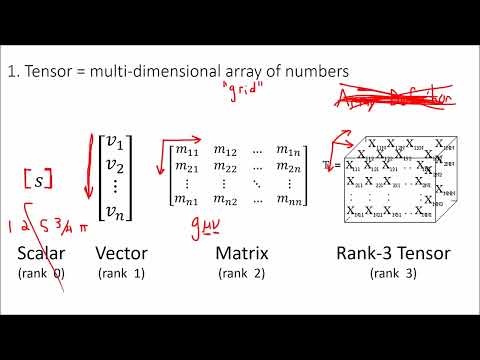
Я предпочитаю изображать тензор в виде вложенных “списков” чисел с любым количеством “уровней”. Другой способ представления: ячейка в электронной таблице Excel, содержащая все данные из другой таблицы. Во второй таблице каждая ячейка связана с другой таблицей и так далее. Каждую таблицу можно рассматривать как дополнительное “измерение”.
Тензор первого порядка имеет только одно измерение. В компьютерных науках это можно назвать вектором или упорядоченным набором чисел. Тензор второго порядка будет матрицей, как электронная таблица в Excel, то есть двумерным. С ростом числа измерений можно рассматривать информацию как векторы, матрицы или массивы, вложенные в массивы, с любым числом измерений (n-мерные).
Вот как можно представить тензор третьего порядка:
Каждая из групп верхнего уровня значений представлена разным цветом. В этом примере цифры каждого значения соответствуют конкретной ячейке значения в общей структуре данных. Крайняя правая цифра каждого значения соответствует группе верхнего уровня, к которой она относится. Все значения красного цвета находятся в группе верхнего уровня номер 1, зелёные — в группе номер 2 и голубые в группе номер 3.
Каждая группа верхнего уровня является матрицей (двумерной). Крайняя левая цифра каждого значения соответствует строке, в которой находится, а средняя цифра — столбцу. Таким образом сохраняется порядок всех значений, что позволяет нам выполнять вычисления на всей структуре, используя другие векторы, матрицы или массивы.
Вот та же структура, содержащая другую информацию:
Каждая буква отображает уникальное положение в структуре; та же цветовая кодировка используется для разграничения матриц верхнего уровня.
Более сложная визуализация возможна с трёхмерным кубом. Каждый вертикальный уровень такого куба будет содержать данные одной из групп верхнего уровня, создавая куб 3x3x3 с 27 уникальными местоположениями. Но возможность визуализировать тензор при помощи графики исчезает, как только мы выходим за пределы трёх измерений.
Из-за этого ограничения давайте рассмотрим, как можно закодировать те же данные, используя компьютерное ПО. С помощью Python и Numpy создадим массив числовых данных из первого примера:
При таком кодировании нам доступно любое количество измерений, что имеет колоссальное значение при работе с гигантскими объёмами сложных данных!
Я надеюсь, у меня получилось объяснить, что, как минимум в машинном обучении, тензоры могут быть представлены в виде вложенных массивов.
Видео:ТЕНЗОРЫ ДЛЯ САМЫХ МАЛЕНЬКИХ ЧАЙНИКОВ (ДЛЯ ФИЗИКОВ)Скачать

 Краткое введение в тензоры
Краткое введение в тензоры
В заметке Магия тензорной алгебры было дано очень неплохое введение в математику тензоров. Но, как мне кажется, этот текст все-равно несколько сложен для понимания. В нем не до конца понятно, что же это такое тензор и зачем он вообще нужен.
Сейчас я попытаюсь дать совсем простое введение в тензоры. Я не претендую на математическую строгость, поэтому некоторые термины могут употребляться не совсем корректно.
Откуда появился термин тензор
Насколько я помню, термин тензор происходит от латинского tensus или английского слова tension — напряжение. Термин возник в процессе осмысления следующей задачи. Пусть нам дано некоторое твердое тело произвольной формы в трехмерном пространстве. К разным концам тела приложены некоторые силы. Как описать возникающие напряжения в некотором сечении этого тела? Ответ на эту задачу — напряжения описываются тензорным полем. Но для понимания этого ответа давайте рассмотрим более простые задачи.
Тензор нулевого ранга
Пусть нам дан в трехмерном пространстве однородный кубик. Давайте его начнем нагревать с какой-либо стороны. Теперь зафиксируем какой-либо момент времени и попробуем описать значения температуры в каждой точке кубика.
Температура — это скаляр, нам нужно только одно число. Введем произвольную систему координат. В рамках этой системы координат температура будет описываться как скалярная функция от (x, y, z).
А давайте теперь возьмем другую систему координат. Что изменится? А ничего! Температура в каждой точке пространства осталась таким же скаляром и при смене системы координат не поменялась.
Вот уже интересно! Мы получили некоторый математический объект, скаляр, который не изменяется при смене системы координат. Назовем его тензором нулевого ранга. Идем дальше.
(Уточнение из комментариев: координаты точек изменятся, но температура в этих точках от поворота системы координат не изменится. Именно температура и есть тензор ранга (0,0))
Тензор первого ранга
Итак, мы нагрели наш однородный кубик. Под действием температуры молекулы какого-либо вещества в нем начали как-то двигаться. Опять зафиксируем какой-либо момент времени и попробуем описать значения скоростей молекул в каждой точке кубика.
Скорость — это вектор. Введем произвольную систему координат. В рамках этой системы скорости в каждой точке пространства будут описываться как векторные функции от (x, y, z). А давайте теперь возьмем другую систему координат? Что изменится? Давайте рассуждать.
Векторное поле скоростей в кубике не изменилось, оно осталось таким же, мы просто взяли другую линейку (другую систему координат) для измерения скоростей. Но изменились компоненты этого вектора. Зная старую и новую систему координат, закон изменения компонент вектора несложно вывести.
Таким образом, мы получили математический объект, вектор, который опять же не изменяется при смене системы координат, но изменяются его компоненты, причем по заранее определенному закону. Это тензор первого ранга. Теперь начинается самое интересное.
Тензор второго ранга
Мы нагрели наш кубик, молекулы начали двигаться. Но представим теперь, что наш кубик перестал быть однородным. Он теперь пористый, внутри состоит из разных каналов с разной ориентацией. Скорость движения молекулы вдоль канала гораздо больше, чем скорость движения поперек канала. Как нам описать такую неоднородную среду?
Зафиксируем какой-либо момент времени, возьмем одну молекулу со своим вектором скорости. Вопрос, как этот вектор скорости изменится в следующий момент времени? Если молекула попала в канал и вектор ее скорости направлен вдоль канала, то скорость не изменится, если вектор направлен поперек канала, то уменьшится в несколько раз, а если под углом, то вектор скорости вообще изменит свое направление.
Это очень похоже на то, что в каждой точке кубика задано нечто, что умеет поворачивать и масштабировать вектора. Да, да, это матрица! Но не произвольная, а специальная, которая не уничтожает вектора, а преобразовывает.
Хорошо, а что будет с нашей матрицей, если мы возьмем другую систему координат, что изменится? Конфигурация каналов в кубике осталась такой же, и эта матрица должна поворачивать вектора скоростей точно таким же образом. Да, компоненты этой матрицы изменятся, но само ее действие на вектора останется таким же.
Таким образом, мы опять же имеем математический объект, матрицу специального вида, действие которой на вектор не зависит от смены системы координат, а ее компоненты пересчитываются по определенному закону. Назовем его тензором второго ранга.
Видео:Вышмат. ТензорыСкачать

 Тензор
Тензор
Часто тензор представляют как многомерную таблицу 

Сам тензор как «геометрическая сущность» от выбора базиса не зависит, что можно наглядно видеть на примере вектора, являющегося частным видом тензора: компоненты вектора меняются при смене координатных осей, но сам вектор — образом которого может быть просто нарисованная стрелка — от этого не изменяется.
Видео:Тензоры 00. Eigenchris. Определение тензоров.Скачать
 Содержание
Содержание
Видео:Лекция №15. Тензоры.Скачать

 Определения
Определения
Современное определение
Тензор ранга 







Сумма чисел 



Тензор как полилинейная функция
Точно так же как ковариантный тензор ранга 









В том же ключе, тензор 




Видео:Тензоры ВведениеСкачать
Компоненты тензора
Выберем в пространстве 





Тогда в пространстве тензоров 

Произвольный тензор 
Используя соглашение Эйнштейна это разложение записывается как
Числа 


Если определить тензор как полилинейную функцию, то его компоненты определяются значениями этой функции на базисе 
О классическом определении
Классический подход к определению тензора, более распространённый в физической литературе, начинает с представления тензоров в компонентах. Тензор определяется как геометрический объект, который описывается многомерным массивом, то есть набором чисел, занумерованных несколькими индексами, или, иначе говоря, таблицей (вообще говоря, 

Так вектор (тензор первого ранга) задаётся одномерным массивом (строкой или лучше — столбцом), а такие объекты как линейный оператор и квадратичная форма — двумерной матрицей. Скаляр же (тензор нулевого ранга) задаётся одним числом (которое можно рассматривать как нульмерный массив с единственным элементом). (Скаляры и векторы удобно рассматривать в качестве частных случаев тензоров, так как все тензорные определения и теоремы для них в силе и векторы со скалярами можно при общем рассмотрении не упоминать отдельно).
Вводятся тензорные операции, которые можно считать прямым обобщением матричных операций (умножение матриц между собой и с векторами), а также векторных операций, таких, как скалярное произведение. Эти операции, если исходить из современного (аксиоматического) определения, прямо вытекают из (поли-)линейности тензоров в этом определении, после разложения векторов, свёртываемых с тензорами, по базису векторного пространства, точно так же, как и матричные операции вытекают из линейности линейных операторов и билинейных форм, представлением каждого из которых в конкретном базисе является конкретная матрица.
С помощью этих операций тензоры связываются с такими фундаментальными геометрическими объектами, как векторы и скаляры, чем, в конечном счёте, определяется их геометрический смысл. Эти же операции связывают тензоры с матрицами преобразований координат (матрицами Якоби). Если речь идёт о тензорном анализе на (римановом или псевдоримановом, с которыми обычно имеют дело в классическом подходе, по крайней мере, на первом этапе) многообразии общего вида, все эти операции определяются обычно общековариантным способом (то есть способом, не зависящим от выбора криволинейных координат) с помощью метрического тензора.
Основными тензорными операциями являются сложение, в этом подходе сводящееся к покомпонентному сложению, аналогично векторам, и свёртка — с векторами, между собой и сами с собой, обобщающая матричное умножение, скалярное произведение векторов и взятие следа матрицы. Умножение тензора на число (на скаляр) можно при желании считать частным случаем свёртки, оно сводится к покомпонентному умножению.
Значения чисел в массиве, или компоненты тензора, зависят от системы координат, но при этом сам тензор, как геометрическая сущность, от них не зависит.
Под проявлениями этой геометрической сущности можно понимать много что: различные скалярные инварианты, симметричность/антисимметричность индексов, соотношения между тензорами и другое.
Например, скалярное произведение и длина векторов не меняется при поворотах осей, а метрический тензор всегда остаётся симметричным. Свёртки любых тензоров с самими собой и/или другими тензорами (в том числе векторами), если в результате не осталось ни одного индекса, являются скалярами, то есть инвариантами относительно замены координат: это общий способ построения скалярных инвариантов.
При замене системы координат компоненты тензора преобразуются по определённому линейному закону.
Зная компоненты тензора в одной координатной системе, всегда можно вычислить его компоненты в другой, если задана матрица преобразования координат. Таким образом, второй подход можно суммировать в виде формулы:
тензор = массив компонент + закон преобразования компонент при замене базиса
Следует заметить, что при этом подразумевается, что все тензоры (все тензоры над одним векторным пространством), независимо от их ранга (то есть и векторы в том числе), преобразуются через одну и ту же матрицу преобразования координат (и дуальную ей, если есть верхние и нижние индексы). Компоненты тензора, таким образом, преобразуются по тому же закону, что и соответствующие компоненты тензорного произведения векторов (в количестве, равном валентности тензора), учитывая ковариантность-контравариантность компонент.
Например, компоненты тензора
преобразуется так же, как компоненты тензорного произведения трёх векторов, то есть как произведение компонент этих векторов
Так как преобразование компонент вектора известно, то таким образом можно легко сформулировать простейший из вариантов классического определения тензора.
Видео:Элементы тензорного анализа. Учебный фильм для вузовСкачать

Примеры
Как следует из определения, компоненты тензора должны меняться определённым образом синхронно с компонентами векторов того пространства, на котором он определён, при преобразовании координат. Поэтому не любая табличка или величина с индексами, выглядящая как представление тензора, на самом деле представляет тензор.
Существуют объекты, которые не только похожи на тензоры, но для которых определены (и имеют разумный и корректный смысл) тензорные операции (свёртка с другими тензорами, в частности, с векторами), однако при этом тензорами не являющиеся:
Видео:Относительность 12 - ТензорыСкачать

Тензорные операции
Тензоры допускают следующие алгебраические операции:
Видео:МСС лекция 4 семестр 2 часть 1 - Тензоры от чайника к чайникамСкачать
Симметрии
В различного рода приложениях часто возникают тензоры с определённым свойством симметрии.
Симметричным по двум ко-(контра-)вариантным индексам называется тензор, который удовлетворяет следующему требованию:


Аналогично определяется косая симметрия (или антисимметричность):


Симметрия или антисимметрия не обязательно должна охватывать только соседние индексы, она может включать в себя любые индексы, учитывая, правда, следующее: симметрия или антисимметрия может относиться только к индексам одного сорта: ко- или контравариантным. Симметрии же, смешивающие ко- и контравариантные индексы тензоров, как правило, не имеют особого смысла, так как, даже если они наблюдаются в компонентах, то разрушаются при переходе к другому базису отнесения (то есть неинвариантны).
Впрочем, в присутствии метрического тензора, наличие операций поднятия или опускания индекса устраняет это неудобство, и ограничение этим по сути снимается, когда тензор представлен подходящим образом (так, например, тензор кривизны Римана 
Эти определения естественным образом обобщаются на случай более чем двух индексов. При этом при любой перестановке индексов, по которым тензор является симметричным, его действие не изменяется, а при антисимметрии по индексам знак действия тензора изменяется на противоположный для нечётных перестановок (получаемых из начального расположения индексов нечётным числом транспозиций — перестановок двух индексов) и сохраняется для чётных.
Существуют и более сложные симметрии, например первое тождество Бьянки для тензора кривизны.
Видео:Тензоры 12. Eigenchris. Тензорное произведение.Скачать

Тензоры в физике
В физике тензоры широко используются в теориях, обладающих геометрической природой (таких, как Общая теория относительности) или допускающих полную или значительную геометризацию (к таковым можно в значительной степени отнести практически все современные фундаментальные теории — электродинамика, релятивистская механика и т. д.), а также в теории анизотропных сред (которые могут быть анизотропны изначально, как кристаллы низкой симметрии, или вследствие своего движения или напряжений, как текущая жидкость или газ, или как деформированное твердое тело). Кроме того, тензоры широко используются в механике абсолютно твердого тела.
Линейные операторы квантовой механики, конечно, также могут быть интерпретированы как тензоры над некими абстрактными пространствами (пространствами состояний), но традиционно такое применение термина тензор практически не используется, как и вообще крайне редко используется для описания линейных операторов над бесконечномерными пространствами. Вообще в физике термин тензор имеет тенденцию применяться только к тензорам над обычным физическим 3-мерным пространством или 4-мерным пространством-временем, или, в крайнем случае, над наиболее простыми и прямыми обобщениями этих пространств, хотя принципиальная возможность применения его в более общих случаях остаётся.
Примерами тензоров в физике являются:
Нетрудно заметить, что большинство тензоров в физике (не рассматривая скаляров и векторов) имеют всего два индекса. Тензоры, имеющие большую валентность (такие, как тензор Римана в ОТО) встречаются, как правило, только в теориях, считающихся достаточно сложными, да и то нередко фигурируют в основном в виде своих свёрток меньшей валентности. Большинство симметрично или антисимметрично.
Простейшей иллюстрацией, позволяющей понять физический (и отчасти геометрический) смысл тензоров, а более точно — симметричных тензоров второго ранга, будет, вероятно, рассмотрение тензора (удельной) электропроводности 









тогда можно для каждой компоненты записать:
И мы увидим, что для любого направления, не совпадающего с 1, 2 и 3, вектор 




Переходя к произвольным декартовым координатам, не совпадающим с этими выделенными направлениями, мы вынуждены будем включить матрицу поворота для преобразования координат, и поэтому в произвольной системе координат соотношение между 

то есть тензор электропроводности будет представлен симметричной матрицей 
Учитывая же то, что удельная мощность тепловыделения 

где 

Таким образом, мы получили (правда, говоря строго, только для случая симметричного тензора) хороший наглядный геометрический образ тензора, применимый в физике. Этот образ состоит из ортогонального базиса (называемого собственным базисом тензора или его собственными координатами), ориентированного в пространстве определенным образом (определяемым свойствами среды, порождающей тензор), и трех (для трехмерного пространства) чисел (коэффициентов), связанных каждое с одной из этих осей (называемых собственными числами или собственными значениями тензора), предназначенных для умножения на них соответствующих компонент вектора, чтобы получить компоненты вектора нового. Как видим, в частном случае 

Или, умножая квадраты этих компонент (компонент в собственном базисе тензора) вектора на собственные числа, и сложив их, получаем скаляр. Поверхности уровня такой квадратичной формы — эллипсоиды. Такой эллипсоид служит также хорошим геометрическим образом тензора. Направление его главных осей — дает собственный базис тензора, а их величины — определяют его собственные числа.
В алгебре же всё сказанное иллюстрирует понятия собственных векторов (собственного базиса) и собственных чисел линейного оператора, квадратичной формы или матрицы, а процесс нахождения собственного базиса и собственных чисел (называемый задачей на собственные значения) называется диагонализацией оператора, квадратичной (или билинейной) формы или матрицы (так как матрица, представляющая оператор или билинейную форму становится в этом базисе диагональной).
📹 Видео
Что такое тензорное произведение матриц? Душкин объяснитСкачать

Тензоры 04. Eigenchris. Что такое ковектор?Скачать

Овчинников А. В. - Линейная алгебра - Понятие тензора. Свойства и операции над тензорамиСкачать

Зубко И.Ю. Тензорный язык - это просто. Часть 1Скачать

ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ АБЕЛЕВЫХ ГРУППСкачать

14.1 Тензоры I. Часть 1Скачать

Тензоры 09. Eigenchris. Метрические тензоры.Скачать

Относительность 18 - Тензор кривизны РиманаСкачать

Бадьин А. В. - Тензорный анализ - Тензорная алгебра (Лекция 1)Скачать

007. Тензорные разложения и их применения — Иван ОселедецСкачать




 Краткое введение в тензоры
Краткое введение в тензоры Тензор
Тензор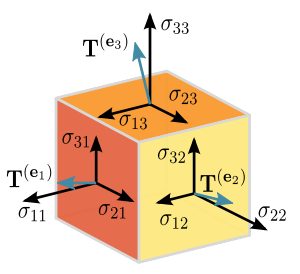

 Содержание
Содержание Определения
Определения























