Факториал на алгоритмическом языке

Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.

Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.

Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:

На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.

Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.

Алгоритм вычисления деревом

Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.

Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).

Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):

P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800

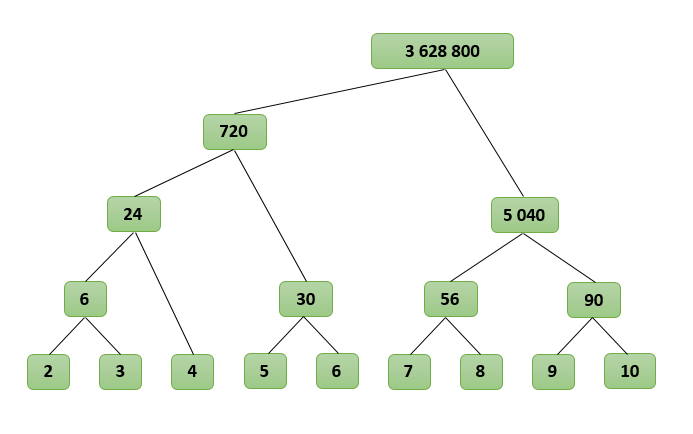
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне

Реализуем описанный алгоритм:

Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.

Алгоритм вычисления факторизацией

Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.

Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:

10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800

Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:

Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!

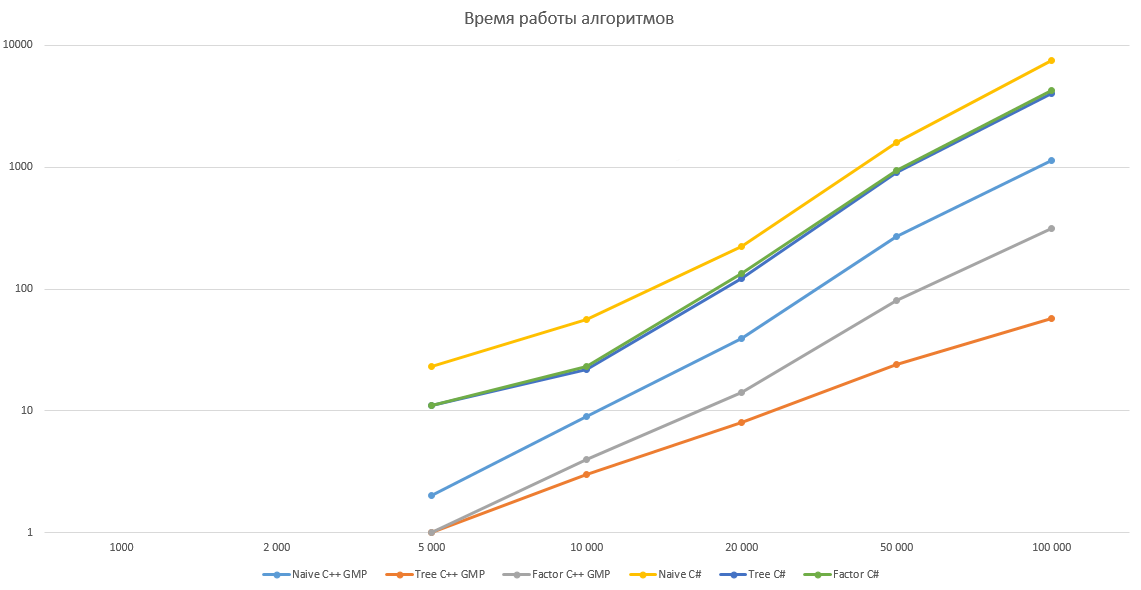
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.

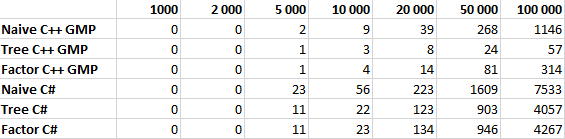
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.

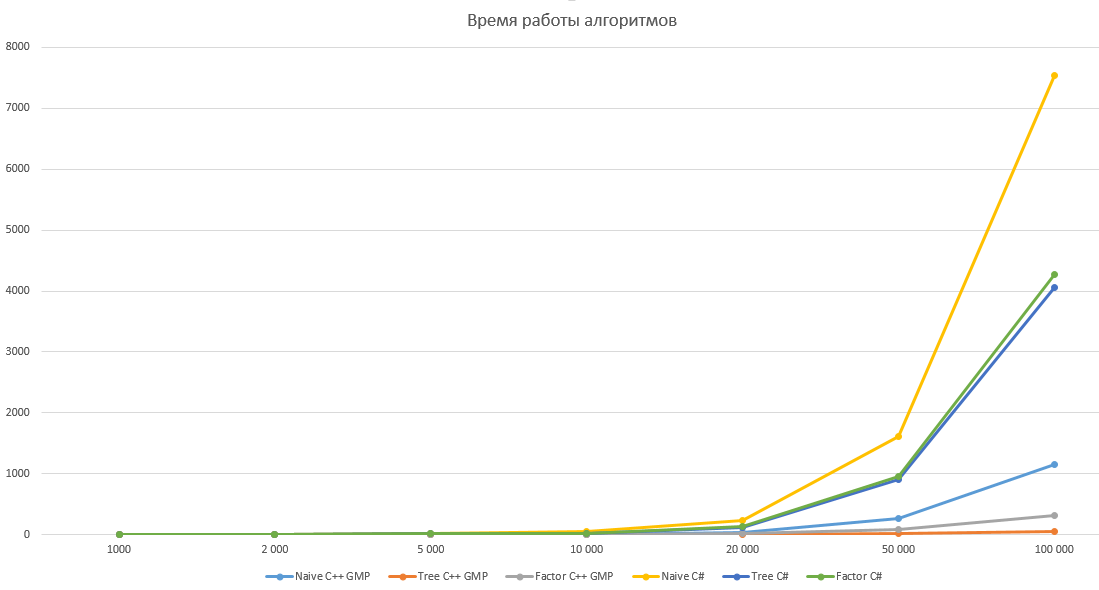
График с линейной шкалой

График с логарифмической шкалой

Идеи и алгоритмы из комментариев

Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них

Исходные коды реализованных алгоритмов приведены под спойлерами

Источник

Видео:АЛГОРИТМЫ в ПРОГРАММИРОВАНИИ для новичков | Левенштейн, Фибоначчи, Факториал и т.д.Скачать

Пятничный JS: единственно верный способ вычисления факториала

Введение

Вычисление факториала — одна из традиционных программистских задач для собеседований. Если вдруг кто забыл, факториал натурального числа N обозначается как N! и равняется произведению всех натуральных чисел от единицы до N включительно. Например, . Казалось бы, что тут сложного? Однако есть свои нюансы.

Например, сравним два самых распространённых способа вычисления факториала.

Многие скажут, что первый способ лучше, но это не так. Во-первых, циклы уже не в тренде, сейчас модно функциональное программирование. Во-вторых, чем больше людей используют второй способ, тем быстрее в основных джаваскриптовых движках появится оптимизация хвостовой рекурсии.

В любом случае, оба эти способа слишком примитивны, чтобы по ним судить о знаниях кандидата. А вот опытный разработчик на React.js уже может написать что-то в этом роде:

Согласитесь, выглядит гораздо солиднее. Впрочем, невооружённым глазом видно, что это всего лишь вариант рекурсивного вычисления. Сходство станет ещё сильнее, если переписать Factorial как функциональный компонент. И, разумеется, я не стал бы писать этот хабрапост, если бы не был готов предложить нечто принципиально новое.

Начнём издалека

Какую из возможностей Javascript недолюбливают и недооценивают сильнее всего? Недолюбливают настолько, что про неё даже придумали специальную поговорку? Конечно же, это eval. Можно сказать, что eval — это тёмная сторона Силы. А как мы помним из фильмов Джорджа Лукаса, нет ничего более крутого и впечатляющего, чем тёмная сторона Силы, поэтому давайте попробуем ей овладеть.

Можно было бы запихнуть в строку какой-нибудь из методов, приведённых в начале поста, а затем передать эту строку в eval, но в этом не было бы новизны. Поставим задачу таким образом, чтобы сделать этот хак невозможным. Пусть у нас есть такой вот каркас:

— и мы хотим, внеся изменения лишь в литерал строки f, сделать так, чтобы функция factorial взаправду вычисляла факториал. Вот задача, достойная истинного ситха.

Что-то это напоминает

Нам нужен код, который возвращает код, который возвращает код… Если забыть про конечную задачу — вычисление факториала, то есть одна хорошо известная штука, которая нам подойдёт. Эта штука называется квайн — программа, которая выводит свой собственный текст.

Про квайны на Хабре написано уже немало, потому я напомню лишь основные принципы квайностроительства. Чтобы сделать простейший квайн, нам нужно:

В строке o.s содержится весь остальной код, а также специальные подстановочные последовательности, начинающиеся с подчёркивания. Страшное выражение внутри console.log заменяет каждую подстановочную последовательность на соответствующее свойство объекта o, что обеспечивает выполнение пунктов 2 и 3 хитрого плана по созданию квайна.

Здесь меня могут поправить: товарищ, это не простейший квайн, а монстр какой-то. Простейший квайн на js выглядит так:

Это правда, но не совсем. Такой квайн считается «читерским», поскольку он из тела функции получает доступ к её же тексту. Это почти то же самое, что прочитать с жёсткого диска файл с исходным кодом программы. Моветон, одним словом.

Скрещиваем ежа с ужом

Как же сделать так, чтобы наш квази-квайн модифицировал сам себя, а в результате превратился в одно-единственное число? Давайте забудем пока про вычисление факториала и постараемся просто написать строку, которая «схлопывается» через определённое количество eval’ов. Для этого нам понадобится:

Обратите внимание на отсутствие return внутри строки: в нём нет необходимости, eval возвращает значение последнего выражения. Запустив этот код в консоли, можно c благоговением наблюдать, как с каждой итерацией цикла значение n уменьшается на 1. Если кто-то скажет, что для такого эффекта достаточно:

— то у него нет чувства прекрасного.

После этого подготовительного этапа уже совсем нетрудно написать итоговую версию вычисления факториала. Просто добавляется ещё одна переменная и чуть усложняется строчка с изменением.

Теперь вы можете смело идти на собеседование.

Заключение

С живым кодом можно поиграться здесь. Как и в прошлой статье из рубрики «Пятничный JS» напоминаю: если вы сделаете что-нибудь подобное на продакшене, то попадёте в ад. С другой стороны, если вы сделаете это на собеседовании, то вам не дадут возможности сделать это на продакшене, и вы не попадёте в ад. Так что делайте это на собеседовании. Спасибо за внимание.

Источник

Видео:Алгоритм нахождения факториала (Factorial algorithm)Скачать

Факториал на алгоритмическом языке

Алгоритмы для вычисления факториала — это алгоритм определения произведения всех натуральных чисел, начиная от единицы и до заданного числа включительно.

Под термином факториал числа понимается функция, которая вычисляет произведение последовательности натуральных чисел от единицы до N включительно: N! = 1 • 2 • 3 • … • N. Факториал является очень быстро увеличивающейся функцией, поскольку даже при относительно малых по величине N, значение его факториала будет уже многоразрядным. Рассмотрим некоторые алгоритмы, позволяющие вычислить факториал числа.

Видео:Вычисление факториала на языке C# (S sharp)Скачать

Наивный алгоритм

Этот алгоритм является самой простой реализацией, так как просто выполняет действия, заложенные в определении факториала:

Готовые работы на аналогичную тему

Рисунок 1. Наивный алгоритм. Автор24 — интернет-биржа студенческих работ

Эта программа выполняется за интервал времени менее двух секунд для N до пятидесяти тысяч. Но есть и более продвинутые алгоритмы и один из них рассмотрим далее.

Видео:Алгоритм нахождение факториалаСкачать

Алгоритм вычисления деревом

Этот алгоритм базируется на таком положении, что операция умножения с числами большой и примерно одинаковой разрядности будет эффективнее умножения большого числа на маленькое. Исходя из этого, необходимо обеспечить при определении факториала примерно равный размер сомножителей на постоянной основе. Пускай требуется вычислить произведение последовательности чисел от L до R. Введём обозначение этого произведения как Р (L, R). Поделим промежуток между L и R на два и вычислим Р (L, R) как P(L, M) • P(M + 1, R), здесь M является серединой чисел L и R, то есть M = (L + R) / 2. Следует отметить, что сомножители получаются примерно одинаковыми. Затем по аналогии разбиваем далее P(L, M) и P(M + 1, R). Эту процедуру необходимо выполнять до тех пор, пока каждый интервал не будет иметь больше двух сомножителей. Понятно, что Р (L, R) = L, когда L и R равны, и P(L, R) = L • R, если L и R имеют единичное отличи. Для того, чтобы вычислить N!, требуется определить Р(2, N). Рассмотрим действие этого алгоритма для N=10, определим Р (2, 10):

( P(2, 4) • P(5, 6) ) • ( P(7, 8) • P(9, 10) )

( (P(2, 3) • P(4) ) • P(5, 6) ) • ( P(7, 8) • P(9, 10) )

( ( (2 • 3) • (4) ) • (5 • 6) ) • ( (7 • 8) • (9 • 10) )

( ( 6 • 4 ) • 30 ) • ( 56 • 90 )

В итоге мы получили подобие дерева, у которого сомножители расположены в узлах, а результирующее значение находится в корневой системе.

Рисунок 2. Дерево. Автор24 — интернет-биржа студенческих работ

Программная реализация этого алгоритма приведена ниже:

Рисунок 3. Программа. Автор24 — интернет-биржа студенческих работ

По этой программе для числа пятьдесят тысяч вычисление факториала длится менее секунды, что в два раза быстрее предыдущего алгоритма.

Видео:Найти факториал числа. Решение задачи на языке программирования PythonСкачать

Алгоритм вычисления факторизацией

Далее с возрастанием степени будет такая же картина. В финале имеем следующую формулу для показателя степени простого сомножителя К:

$N / K+ N / K^2 + N / K^3 + N / K^4 +…$

Для примера определим, сколько раз двойка в различных степенях входит в факториал десяти. Число два содержится в каждом втором сомножителе (2, 4, 6, 8 и 10). А общее число этих сомножителей 10 / 2 = 5. При этом, каждый четвёртый множитель выдаёт число четыре (то есть два в степени два). Этих сомножителей 10 / 4 = 2 (4 и 8). Далее восьмой сомножитель даёт число восемь (то есть два в степени три). Такой сомножитель только один 10 / 8 = 1 (8). Два в четвёртой степени — это число шестнадцать. Но его нет ни в одном сомножителе, следовательно, алгоритм можно останавливать. В итоге видим, что степень числа два при разложении факториала десяти на простые сомножители равняется 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.

Источник

Видео:Вычисление факториала на языке C++Скачать

Самый быстрый факториал

Столкнулся с интересной задачкой. Как посчитать факториал числа самым быстрым способом? Быстрее чем за O(n). Подкиньте идею.

Видео:Рекурсия. Факториал числа c++ рекурсивно. Рекурсия факториал. Рекурсивный алгоритм факториал. #44Скачать

8 ответов 8

Видео:ФакториалСкачать

Типы со знаком (signed)

Видео:Алгоритм нахождения факториала | от университета к кремниевой долиныСкачать

Типы без знака (unsigned)

Для unsigned int всё интереснее, он может переполняться, но fac(34) имеет множитель 2^32:

Поэтому начиная с 34 все результаты fac(uint32_t) будут равны нулю.

Видео:Java урок - 9.2 Рекурсия. Задача нахождения факториала числа nСкачать

64-разрядные типы

Таким образом, использование таблицы факториалов из 66 элементов покроет всех типы до 64 разрядов:

Вот есть интересная статейка. Там предлагают считать факториал за O(loglogn*M(nlogn)) (где M(n) — время перемножения двух n-значных чисел). Быстрее вряд ли получится.

Также гляньте вот эту статью — там считают факториал по простому модулю.

Есть интересные материалы по этому поводу. Во-первых, есть калькулятор факториалов на JavaScript. Он мгновенно вычисляет факториалы чисел до 9.999.999.999

Там же есть материалы по алгоритмам факториалов: http://www.luschny.de/math/factorial/FastFactorialFunctions.htm. Я думаю, тут действительно хорошие алгоритмы 😉

На этом же сайте описывается некий метод, который, как я понял использовался в калькуляторах HP. Некий RPN-калькулятор.

Думаю, что самый быстрый алгоритм вычисления факториала определяется структурой вычислительных средств.
Например, формула Стирлинга допускает представление вида
n!

Ну я такой вариант сочинил.

Вопрос очень быстро решается при помощи гугла, ответ взят с сайта algolist.manual.ru:

Вот приближение десятичного логарифма факториала:

Целая часть этого покажет количество знаков числа-1, а с мантиссой можно работать.

Можно вычислять факториал как eln(n!), и это будет быстрее, чем прямое умножение. Но это не будет точное значение для больших значений n, где есть реальный выигрыш в скорости.

Тем не менее, часто(например, в вычислении биномиальных коэффициентов) нам нужен не сам факториал, а некое значение, получающееся в результате деления громадного факториала на другие числа того же порядка, и в результате получается небольшое число.

В этом случае имеет смысл оперировать именно с логарифмом факториала, который вычисляется (как видно, например, из исходника выше) гораздо проще и быстрее. Деление и умножение будут заменены разностью и суммой логарифмов. Если нужны реально эффективные вычисления, то такой путь при контроле точности вычислений, безусловно, предпочтительнее.

Источник

Видео:Факториал числа 10 - NumberphileСкачать

Сколькими способами можно записать факториал на Scheme?

Рассмотрим некоторые возможные способы записи вычисления факториала. Заодно получится своеобразная ода языку программирования Scheme. Думаю, этот замечательный язык того вполне заслуживает.

У меня получилось 10 вариантов записи определений функций, которые можно свести к 3 основным способам вычисления: традиционному линейно-рекурсивному вычислительному процессу, итерации, генерации последовательности чисел с последующей сверткой умножением. Предлагаю рассмотреть эти варианты подробнее. Попутно мы рассмотрим: оптимизацию хвостовой рекурсии, функции высших порядков и метапрограммирование, отложенные вычисления, бесконечные списки, мемоизацию, способ создать статическую переменную в Scheme и гигиенические макросы.

Для экспериментов был использован старый добрый диалект Scheme R5RS и популярный принцип изобразительного искусства «минимум средств — максимум впечатлений».

Все примеры на Scheme были подготовлены в среде DrRacket 6.2 в режиме R5RS. Замеры времени выполнения были выполнены в Guile 2.0 в среде ОС OpenSUSE Leap 15.

Для начала можно взять рекурсивное определение факториала и просто переписать формулу на Scheme:

Получилось определение функции (в терминах Scheme — процедуры, хотя по-сути она является функцией) для вычисления факториала, которое можно увидеть в бесчисленном множестве руководств по программированию, начиная с бессмертной книги Х. Абельсона и Д. Сассмана «Структура и интерпретация компьютерных программ».

Читать и понимать этот код можно так: факториал есть если , иначе — . Таким образом, этот код соответствует рекурсивному определению факториала, принятому в математике. Единственное, мы не проверяем принадлежность неотрицательным числам.

Будучи рекурсивным, код выше содержит очевидное ограничение на величину : на стеке будут накапливаться данные рекурсивных вызовов, пока не достигнет 0. Это может вызвать переполнение стека при больших .

Как можно снять это ограничение? Надо оптимизировать хвостовую рекурсию: переписать код таким образом, чтобы рекурсивный вызов стал хвостовым (т.е. последним в процедуре). Это позволит интерпретатору Scheme выполнить оптимизацию — заменить рекурсивное вычисление итеративным.

Если воспользоваться рекомендациями авторов упомянутой выше книги, можно получить следующее:

Этот код является расхожим примером, и, начиная с книги «Структура и интерпретация компьютерных программ», именно на нем обычно объясняют оптимизацию хвостовой рекурсии.

Scheme славится своим удобством для символьных вычислений в силу «единства кода и данных» (так иногда говорят о языках семейства Лисп). Используем эту особенность: сформируем выражение для вычисления факториала числа , а затем его вычислим:

Scheme поддерживает отложенные вычисления. Haskell, который испытал значительное влияние Scheme, использует ленивую модель вычислений, т.е. не вычисляет значение выражения до тех пор, пока результат этих вычислений не будет востребован. Это позволяет иметь в программах такие своеобразные структуры данных, как бесконечные списки. Если из них брать только часть, необходимую для дальнейших вычислений, программа не будет зацикливаться:

На Haskell получение из бесконечного списка можно записать так:

Используя пару форм Scheme delay / force попробуем сделать нечто подобное. Ключевое слово delay создает обещание вычислить значение выражения. Ключевое слово force распоряжается осуществить эти вычисления, полученное значение вычисляется и запоминается. При повторном обращении новых вычислений не производится, а возвращается значение, вычисленное ранее.

Конструктор ленивой пары lazy-cons реализован в виде макроса. Это сделано для того, чтобы избежать вычисления значения второго элемента пары при ее создании.

Идея состоит в том, чтобы создать бесконечный список значений, а потом взять из него то, которое нужно. Для этого определим ленивую версию процедуры для получения элемента по индексу:

Здесь n! и n+1 — имена переменных. В Scheme, по-сравнению с другими языками, существует очень немного символов, которые нельзя использовать в идентификаторах.

Обратите внимание, что генератор бесконечного списка generate-factorials не содержит выхода из рекурсии. Тем не менее, он не будет зацикливаться, так как при его вызове будет вычисляться только голова списка, хвост же будет представлен обещанием вычислить значение.

Теперь можно определить как получение -го элемента списка факториалов:

Это работает. При этом, если в одной сессии интерпретатора вычислять факториалы различных чисел, то вычисления будут происходить быстрее, чем в строгих версиях, ведь часть значений в ленивом списке будет уже вычислена.

Кстати, для повышения производительности можно применить запоминание уже вычисленных значений — мемоизацию. Будем хранить вычисленные значения в ассоциативном списке, в котором ключами будут числа, а значениями — их факториалы. При вызове, просмотрим список на предмет уже вычисленных значений. Если значение присутствует в списке, будем возвращать это сохраненное значение. Если значение в списке отсутствует, будем вычислять его, помещать в список, и только потом возвращать. Чтобы этот список всегда находился при вызываемой функции, а не в глобальном окружении, разместим его в статической переменной:

является принятым в Scheme способом создать процедуру со статической переменной. Принцип такого объявления удобно пояснить на более коротком примере — процедуре, возвращающей число своих вызовов:

В одной сессии интерпретатора первый вызов (count) вернет 1, второй — 2, третий — 3 и т.д. Как это работает?

Без синтаксического сахара определение count выглядит так:

Данная реализация также обещает прирост производительности при неоднократном вычислении факториалов различных чисел в одной сессии интерпретатора.

Разумеется, здесь также возможна оптимизация хвостовой рекурсии:

Конструкция do — достаточно универсальная, и именно поэтому — не слишком удобочитаемая. Не лучше ли организовать свой собственный цикл в императивном стиле? В этом помогут макросы:

Благодаря оптимизации хвостовой рекурсии интерпретатором, получим цикл, к каким мы привыкли в императивных языках программирования. Благодаря оптимизации хвостовой рекурсии, стек расти не будет.

Определение факториала с использованием for :

Отсюда, шаблоном синтаксического правила будет сформирован следующий код:

Возможен еще один вариант, внешне похожий на императивный цикл for — со встроенной процедурой for-each :

Велик и могуч язык Scheme! А что с производительностью?

Для замеров производительности воспользуемся GNU Guile — в этой среде можно замерить время вычисления выражения наиболее просто.

Guile работает следующим образом: компилирует исходный текст программы в байт-код, который затем выполняется виртуальной машиной. Это — только одна из реализаций и один из нескольких возможных способов выполнения программы на Scheme, существуют и другие: Racket (использует JIT-компиляцию), Chicken Scheme (использует «честную» интерпретацию или компиляцию в подмножество C) и т.д. Очевидно, что и ограничения, и производительность программ в этих средах могут несколько отличаться.

Замеры будем производить при некотором значении . Каким должно быть это ? Таким, с каким наибольшим смогут «справиться» предложенные варианты. С настройками Guile 2.0 по-умолчанию, на ПК с Intel Core i5 и 4 Гб ОЗУ, меня получилось следующее:

Процедура	Проблема
factorial-classic	переполнение стека при 10,000$» data-tex=»inline»>
factorial-classic-tco	нет ( )
factorial-fold	переполнение стека при 10,000$» data-tex=»inline»>
factorial-eval	переполнение стека при 8,000$» data-tex=»inline»>
factorial-lazy	при использует раздел подкачки и зависает
factorial-memoized	переполнение стека при 10000$» data-tex=»inline»> только при первом запуске
factorial-memoized-tco	при 1,000$» data-tex=»inline»> использует раздел подкачки и зависает
factorial-do	нет ( )
factorial-for	нет ( )
factorial-for-each	нет ( )

Отсюда, тесты производительности выполнялись при . Результаты представлены в таблице ниже, где — время выполнения, — время работы сборщика мусора в секундах.
Для всех процедур, кроме ленивых и мемоизованных, указаны наименьшие значения времени выполнения и соответствующее ему время работы сборщика мусора, полученные по итогам трех запусков при .
Для мемоизованных и ленивых процедур указано время выполнения первого вызова, далее — меньшее из трех вызовов.

Процедура	, с	, с	Примечания
factorial-classic	0,051	0,034
factorial-classic-tco	0,055	0,041
factorial-fold	0,065	0,059
factorial-eval	0,070	0,040
factorial-lazy	0,076	0,036	первый вызов
factorial-lazy	0,009	—	последующие вызовы
factorial-memoized	0,077	0,041	первый вызов
factorial-memoized	0,002	—	последующие вызовы
factorial-memoized-tco	0,077	0,041	первый вызов
factorial-memoized-tco	0,002	—	последующие вызовы
factorial-do	0,052	0,025
factorial-for	0,059	0,044
factorial-for-each	0,066	0,042

У нас есть 4 варианта, которые могут работать с большими . При они имеют следующие времена вычисления и сборки мусора:

Процедура	, с	, с
factorial-classic-tco	8,468	6,628
factorial-do	8,470	6,632
factorial-for	8,440	6,601
factorial-for-each	9,998	7,985

Можно видеть, что при не слишком больших наиболее быстрым и, одновременно, самым коротким и оказывается первый. Этот же вариант наиболее полно соответствует математическому определению факториала. Вариант с оптимизацией хвостовой рекурсии ему не сильно уступает в производительности. Оба этих варианта являются идиоматическими, рекомендованными авторами языка. Вывод во многом очевиден: если не оговорено иное, подход, являющийся для языка «типовым», является предпочтительным, по-крайней мере, для первой реализации алгоритма или метода.

В то же время, язык Scheme позволил написать нам много вариантов реализации вычисления факториала, используя при этом весьма ограниченный набор примитивов (то самое «минимум средств — максимум впечатлений»). Поэтому, несмотря на почтенный возраст и не слишком широкую распространенность, этот язык всё ещё можно рекомендовать для исследовательского программирования: похоже, на нем можно реализовать всё что угодно и каким угодно (и каким удобно) способом.

Источник

💡 Видео

C++. Факториал с помощью рекурсииСкачать

39 Задача: Вычислить факториал при помощи PythonСкачать

Что такое факториал | МатематикаСкачать

Комбинаторика: перестановка, размещение и сочетание | Математика | TutorOnlineСкачать

ФакториалСкачать

Алгоритмы и структуры данных JavaScript. Вычисление факториала. Урок #1Скачать

Вычислить #ФАКТОРИАЛ ЧИСЛАСкачать

Основы Java. Урок 027. Рассчитываем факториал.Скачать

Факториал 0! - Numberphile на русском.Скачать