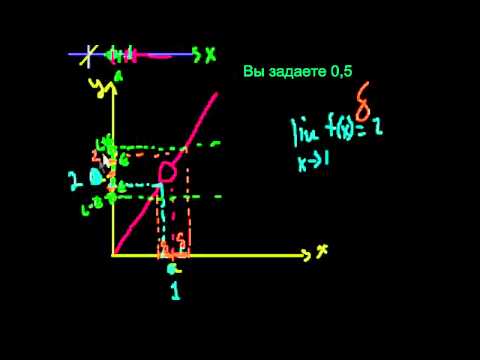
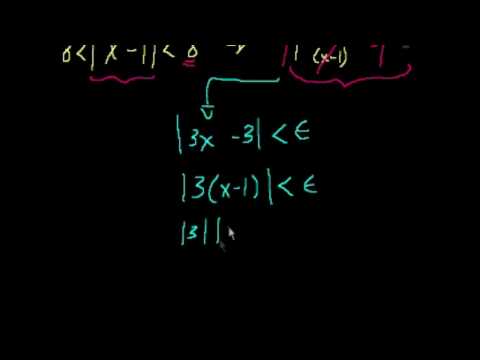5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке «эпсилон-дельта» и языке пределов, равномерная непрерывность.
Если каждому значению n = 1,2,… ставится в соответствие по некоторому закону вещественное число xn, то множество занумерованных вещественных чисел x1, x2,…, xn. = <xn> называется числовой последовательностью. Это частный случай функции, аргумент которой принимает дискретные значеня.
Число A называется пределом последовательности при
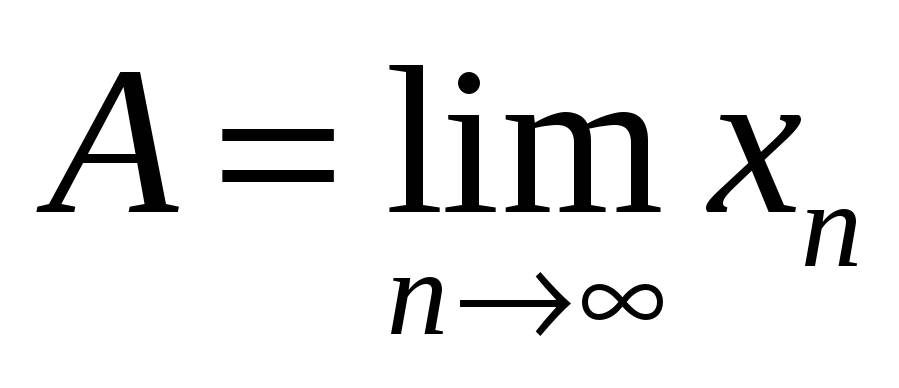

В любой окрестности точки A находятся все члены последовательности, начиная с некоторого номера.
Если существует конечный 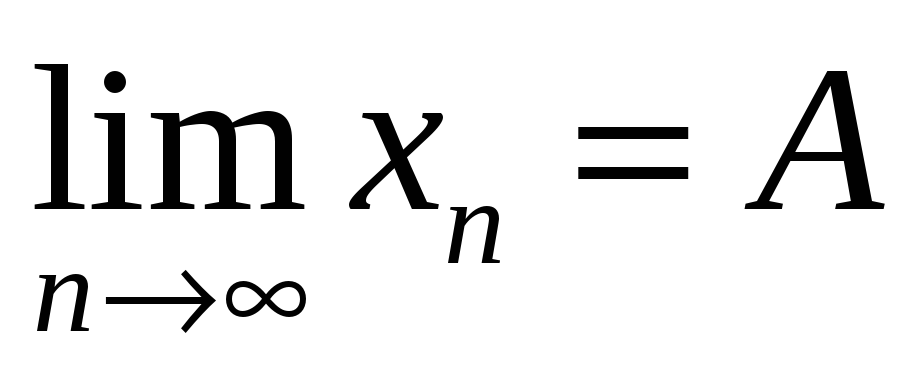
Точка x0 называется предельной точкой множества M, если в окрестности x0 содержится бесконечное множество точек множества M.
Если последовательность имеет несколько предельных точек, то значение самой большой предельной точки называется верхним пределом последовательности 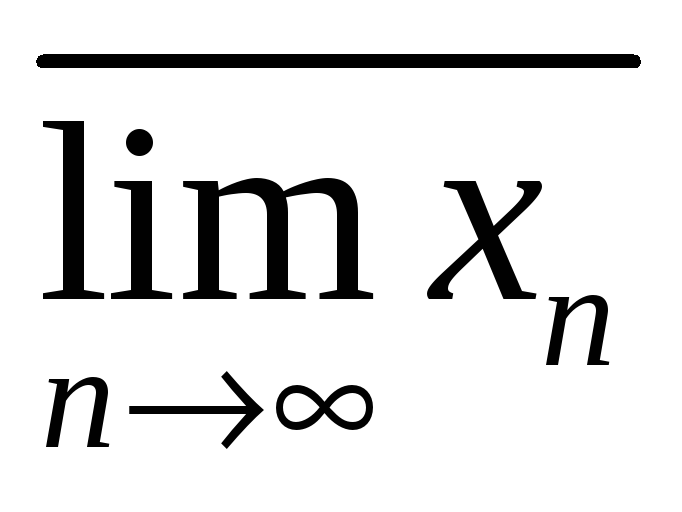
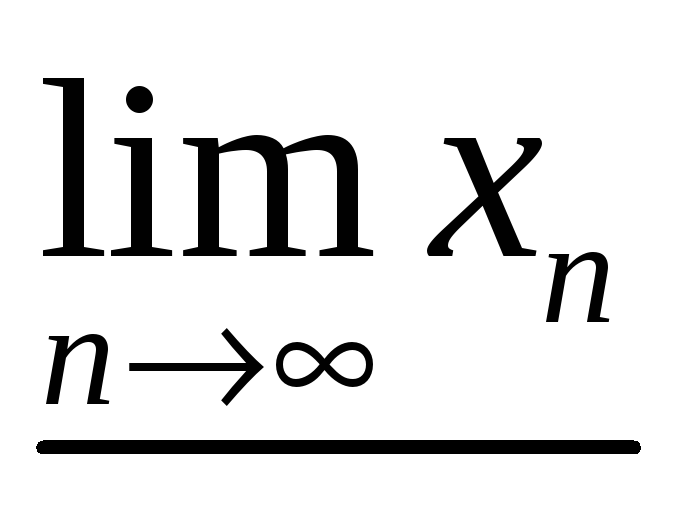
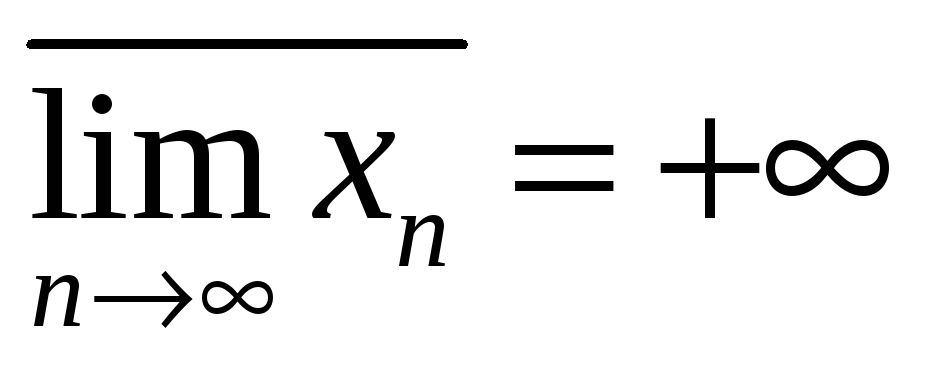
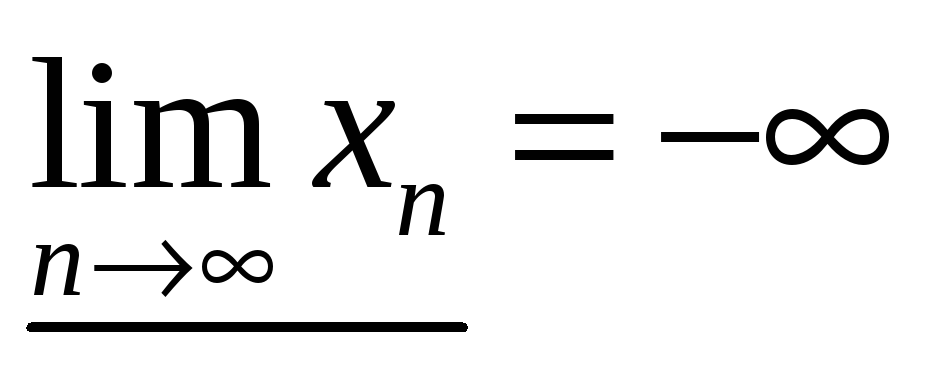
Последовательность может быть сходящейся, только если она имеет единственную точку (число).
Последовательность называется ограниченной, если M>0, что для
Т: Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Т: Если последовательность сходится, то она является ограниченной. Обратное неверно.
Но не сходится, так как 2 предельные точки
Если 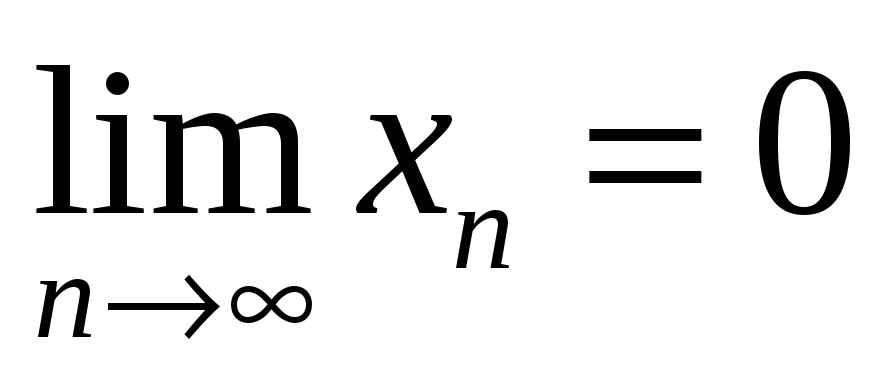
Если 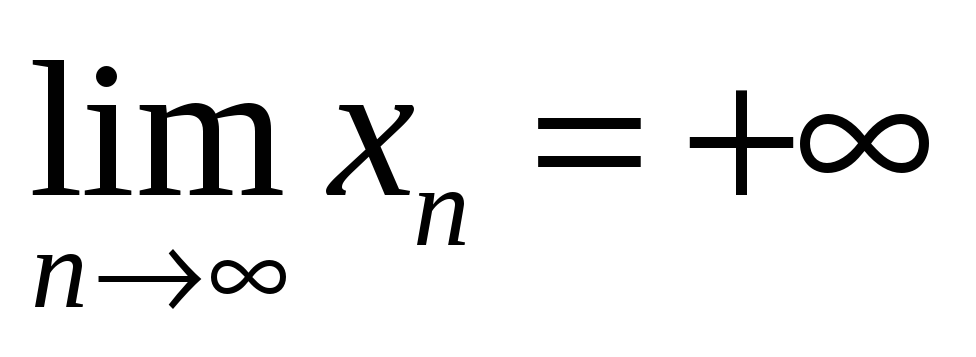
Связь неограниченная 
бесконечно большая неограниченная. Обратное не верно:
не бесконечно большая
Функцией y = f(x) называется закон, по которому каждому значению xD(f)R ставится в соответствие единственное действительное число yR.
При этом множество значений аргумента D(f) называется областью определения функции, а множество значений <y | y = f(x), xD(f)> называется множеством значений функции.
Функция может быть задана аналитически (то есть формулой), таблично или графически.
Если функция задана таблично, то чтобы найти значение функции для промежуточных значений аргумента применяют интерполяцию, заменяя функцию линейной, квадратичной на участке между двумя значениями аргумента.
Пусть точка x0 является предельной точкой области определения функции, тогда
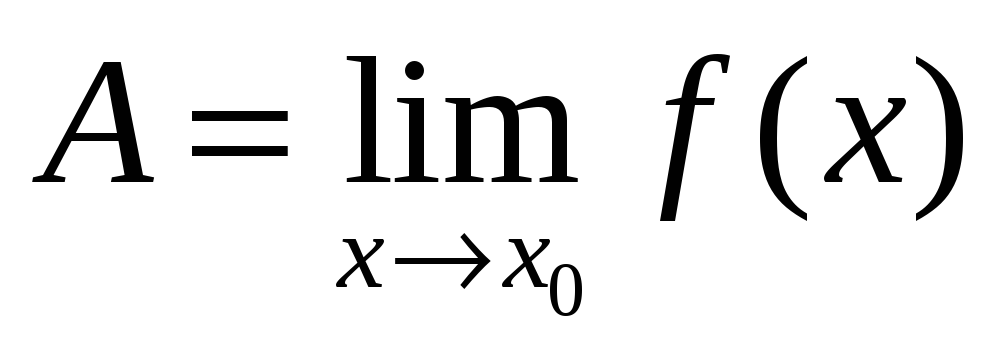
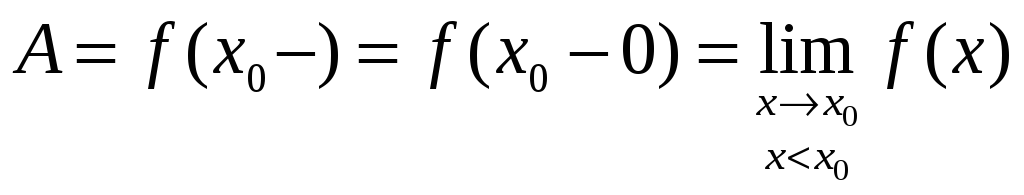
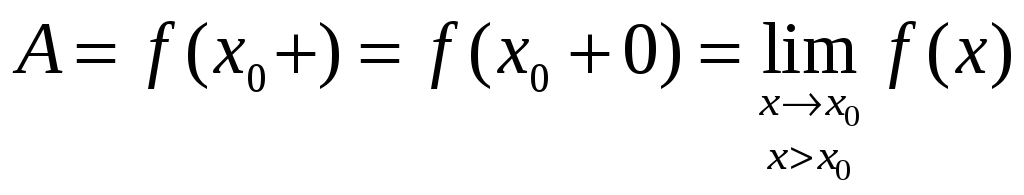
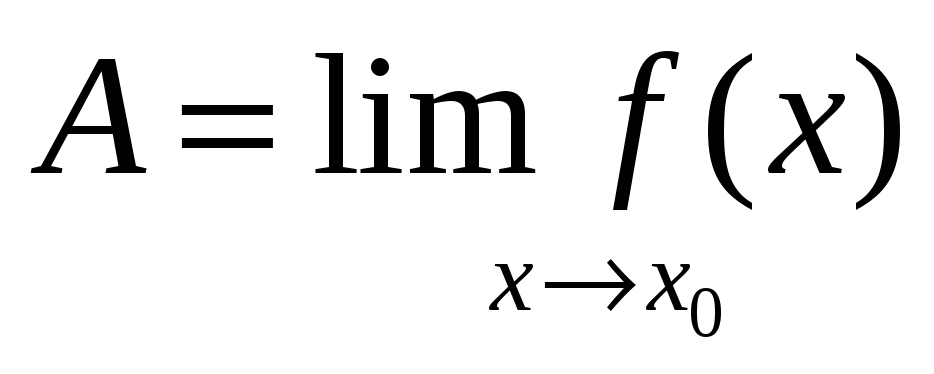
Функция f(x) называется непрерывной в точке x0, если:
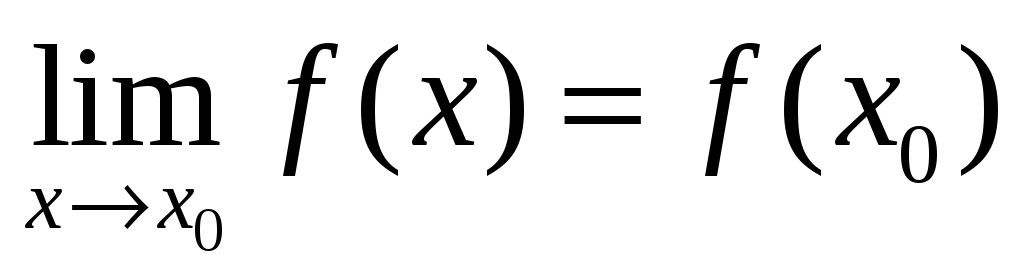
На языке пределов: функция f(x) называется непрерывной в точке x0, если она:
1) определена в этой точке;
2)
На языке ε и δ: функция f(x) называется непрерывной в точке x0, если:
1)
1. Если x0 является предельной точкой D(f)
f
Если функция непрерывна в каждой точке множества X, то она непрерывна на множестве X.
Сумма 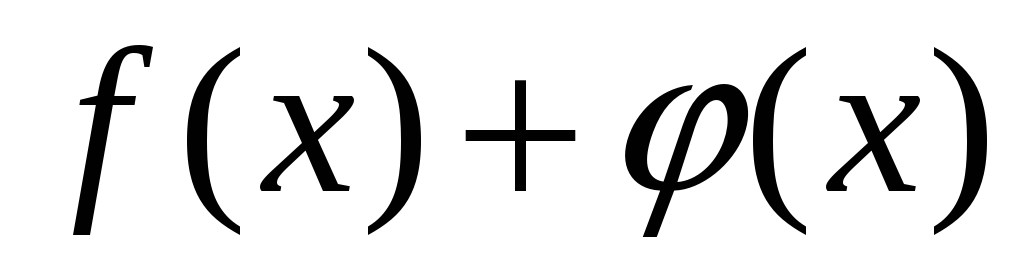
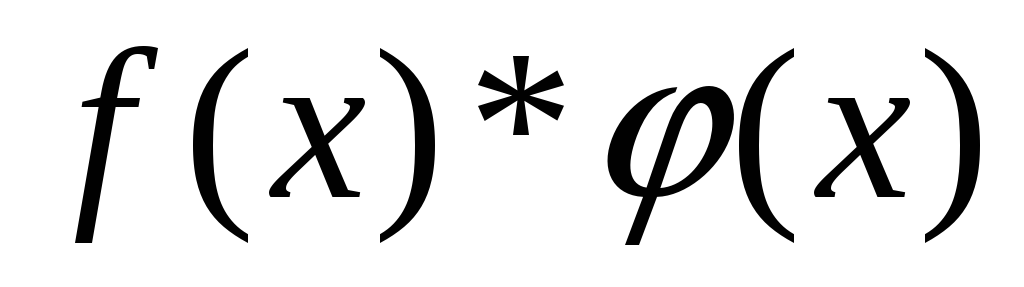
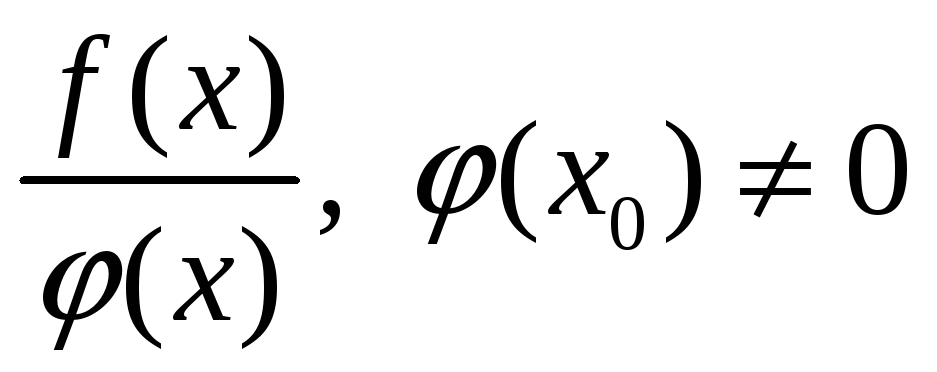
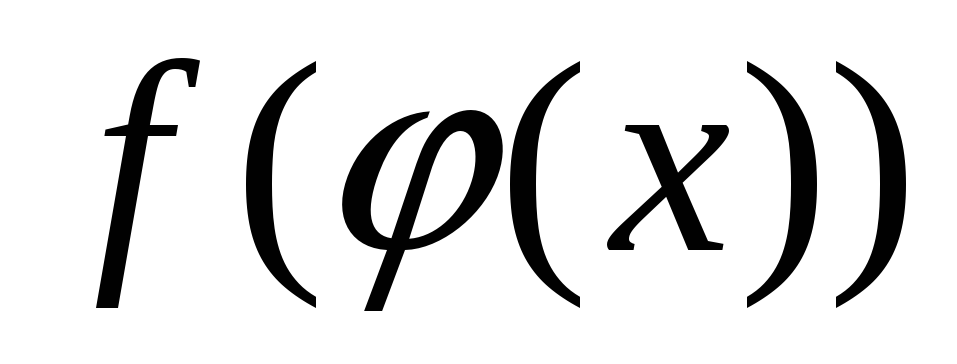
Все элементарные функции непрерывны в своей области определения
Элементарные функции из основных элементарных получаются с помощью конечного числа операций сложения, деления, умножения, суперпозиции.
Исследовать на непрерывность, точки разрыва
Функция элементарна. В своей области определения непрерывна
0 – предельная точка для ОДЗ. Но функция не определена в 0 
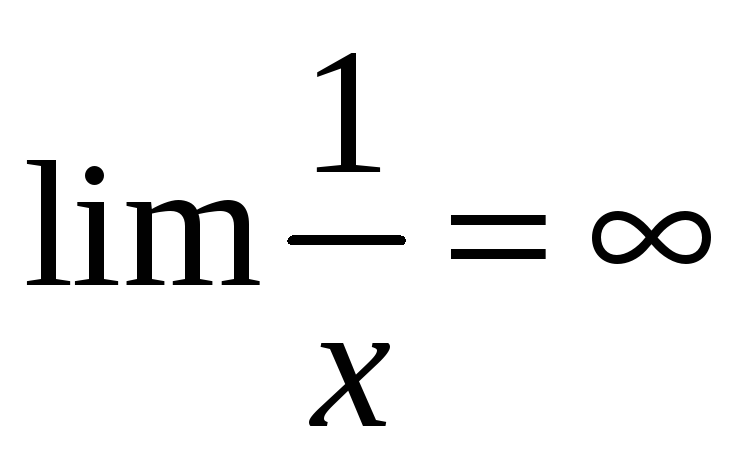
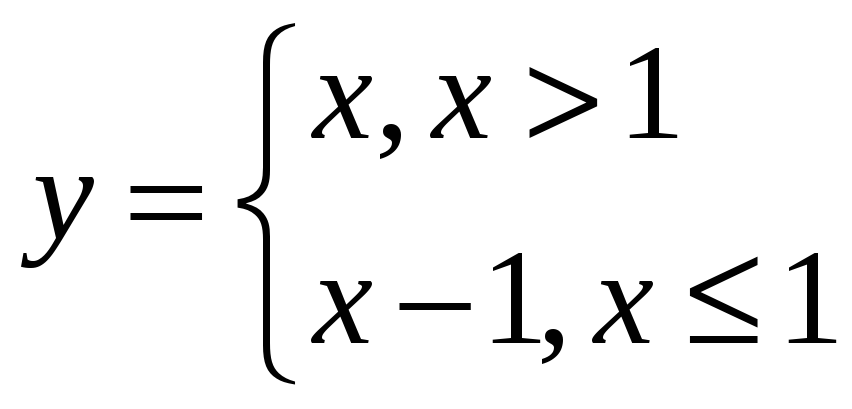
Определение непрерывности функции по Гейне
Функция непрерывна в точке x0, если:
1. она определена в точке x0, то есть 
2. для 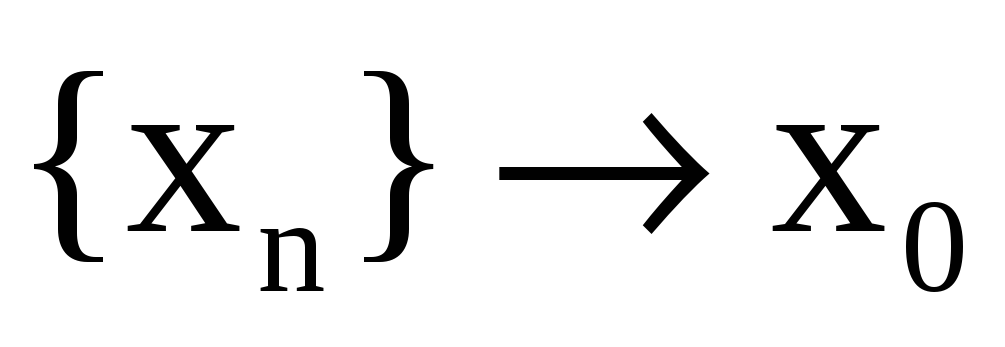
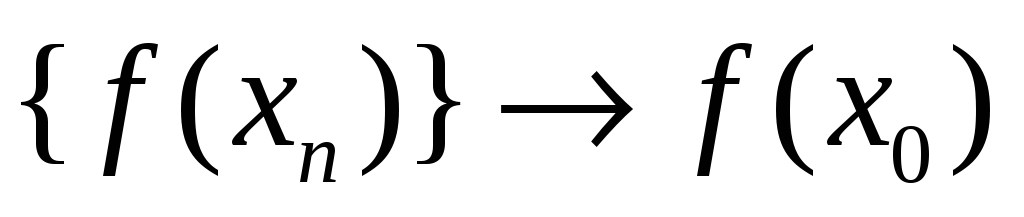
Функция Дирихле определена, но разрывна во всех точках
Видео:[Calculus | глава 7] Пределы, правило Лопиталя и эпсилон-дельта определениеСкачать
![[Calculus | глава 7] Пределы, правило Лопиталя и эпсилон-дельта определение](https://i.ytimg.com/vi/gCyRR20hcew/0.jpg)
 Язык эпсилон дельта для чайников
Язык эпсилон дельта для чайников
Французский писатель Альфонс Алле (1854–1905) говорил:
«Бесконечность велика, особенно ближе к концу»,
тем самым не без доли юмора показав, что мы не можем воспринимать бесконечность как таковую и всегда представляем её в сравнении с чем-либо. Иными словами, человек может рассматривать бесконечность только в привязке к чему-то конечному, так как сам имеет конечную природу. Когда мы смотрим вдаль, мы теряемся и погружаемся в философские размышления, домыслы и гипотезы и, в лучшем случае, формируем к бесконечности какое-то отношение, не всегда рационально обоснованное. Поэтому неудивительно, что бесконечность была, есть и будет темой философских, научных и религиозных споров, ведь философия, наука и религия — три огромные области человеческой мысли, границы между которыми не всегда чётко определены.
Когда большинство людей думают о бесконечности, они испытывают головокружение, ведь она неизменно ускользает от нас, как бы мы ни старались. И это в самом деле так. Возможно, бесконечность именно потому вызывает такой интерес, что представляет собой неисчерпаемый источник вдохновения. История её изучения в математике настолько любопытна, что можно говорить о «математике бесконечности» и смело утверждать, что в математике бесконечность перестала быть чем-то неясным и превратилась в полноценный математический объект, подобный числам и геометрическим фигурам.
Но любой математический объект должен быть чётко определён. В этом смысле математик подобен охотнику: он исследует незнакомую местность, выслеживает добычу, выжидает, берёт её на мушку и, тщательно прицелившись, стреляет.
Это же произошло и с бесконечностью, причём она была непростой добычей — потребовалось больше трёх тысяч лет, чтобы поймать её. В погоне за бесконечностью учёным пришлось петлять между догмами и парадоксами, вступать на территорию греческой философии, разбираться в хитросплетениях религиозных измышлений и секретов тайных обществ. Однако бесконечность можно было встретить и в геометрии, и в лабиринте чисел, более привычных охотникам-математикам.
Мы проследим, как размышляли о бесконечности величайшие мудрецы всех времён и народов, будь то философы, богословы, физики или математики. В погоне за бесконечностью некоторые из них утратили рассудок, другие поплатились жизнью, взойдя на костёр по приговору инквизиции, и всё это — из-за идеи. Однако мы знаем, что одна идея способна радикально изменить наше восприятие мира и пошатнуть основы верований.
Эта тема интересует не только математиков, но и философов, при этом и математическая, и философская точка зрения на бесконечность должны быть согласованы между собой. Ведь, как сказал французский математик Жан-Шарль де Борда (1733–1799),
«без математики нельзя глубоко проникнуть в суть философии, без философии нельзя глубоко проникнуть в суть математики, а без них обеих нельзя понять суть чего бы то ни было».
Глава 1. Что такое бесконечность
Понятие бесконечности — это неотъемлемая часть человеческой мысли. Весьма вероятно, что мы имеем некое врождённое неясное представление о бесконечности, которое постоянно сопоставляем с противоположным ему чётким представлением о конечности, являющейся частью нашей природы. В философии и богословии размышления о бесконечности могут быть необязательными и ситуативными, но в математике её исследование всегда было и остаётся насущной необходимостью.
Бесконечность в повседневной жизни
Известен анекдот о некоем преподавателе математики, которому нужно было в первый раз объяснить студентам, что такое бесконечность. Он взял коробку с мелками, достал один и начал рисовать прямую на доске. Дойдя до края доски, он продолжил вести линию по стене, затем по полу и, не останавливаясь, вышел из аудитории и исчез из вида в конце коридора, продолжая вести линию. Удивлённые студенты ждали, что будет дальше. Спустя некоторое время прозвенел звонок к концу лекции.
Преподаватель исчез. Последним, кто его видел, был вахтёр. Преподаватель шёл по улице и, не отрывая мела от асфальта, по-прежнему чертил линию. Прошло три дня, и руководство университета решило найти преподавателю замену. Через несколько месяцев, к удивлению студентов, преподаватель вернулся. Он оброс бородой, за спиной у него был рюкзак, в руке он держал кусочек мела. Он вошёл в класс, по-прежнему чертя на полу линию, дошёл до доски и, наконец, остановился.
Усталый преподаватель повернулся к студентам и сказал: «Эта линия невероятно велика, но она — ничто в сравнении с бесконечностью».
Неизвестно, какое решение приняло руководство университета — возможно, преподавателя поместили в лечебницу. Также неизвестно, поняли ли студенты, что такое бесконечность. Однако преподавателю удалось выразить одно: бесконечность неизбежно связана с чем-то исключительным и даже шокирующим.
Я впервые осознал, что такое бесконечность, ребёнком, когда оказался между двумя параллельными зеркалами в кабине лифта. «Что это?» — спросил я. Отец взял меня за руку и ответил: «Это бесконечность». С тех пор бесконечность для меня подобна далёкой, удивительной и пугающей стране, по которой лучше всего путешествовать, если кто-то держит тебя за руку.
Для всех нас бесконечность находится где-то далеко, в совершенно недостижимом месте, и в лучшем случае вызывает страх, в худшем — безмерный ужас. Однако альтернатива бесконечности также не слишком обнадёживает. Если Вселенная конечна, что находится за её пределами? Ответ: Ничто, с большой буквы. И это «Ничто» ещё невероятнее, чем бесконечность.
Иллюстрация Гюстава Доре к «Аду» — первой части «Божественной комедии» Данте Алигьери. Дантовский ад был синонимом бесконечных страданий и вечных мук.
Определение из словаря
По определению из словаря, «бесконечность» обозначает нечто чрезмерно великое, необычайно большое или продолжительное. Однако мы часто используем это слово, говоря «бесконечное пространство», «бесконечно много раз», «бесконечное время», «бесконечное терпение». Все мы понимаем смысл этих выражений, но если мы попробуем разобраться, что же имеется в виду на самом деле, то увидим, что наши способности размышлять о бесконечности ограничены, и мы быстро переходим к банальностям и клише, которые никак не помогают нам приблизиться к пониманию сути бесконечности. Это понятие имеет философскую природу: размышлять о бесконечности означает философствовать, а для таких размышлений нужно иметь какую-то отправную точку. Проще всего будет обратиться к словарю.
В толковом словаре русского языка слово «бесконечность» имеет четыре значения.
1. Отсутствие конца, предела наличию каких-либо однородных объектов в пространстве или последнего момента осуществления каких-либо процессов.
Видео:Предел ФУНКЦИИ по КОШИ (определение). Язык "эпсилон - дельта"Скачать

 Язык эпсилон дельта символы
Язык эпсилон дельта символы
| ◄ | ΐ | Α | Β | Γ | Δ | Ε | Ζ | Η | Θ | ► |
| ◄ | ΰ | α | β | γ | δ | ε | ζ | η | θ | ► |
δ: greek small letter delta
δ: U+03B4
Видео:Определение предела на языке эпсилон-дельта 2Скачать

![Язык эпсилон дельта для чайников Язык эпсилон дельта для чайников: Использование [ править | править код ]](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20768%20768'%3E%3C/svg%3E) Использование [ править | править код ]
Использование [ править | править код ]
Прописная буква Δ используется как символ для обозначения:
Строчная буква δ используется как символ для обозначения:
Также с греческой буквой сходны другие символы, употребляемые в математике:
задан 25 Фев ’17 22:40
Романенко
183 ● 2 ● 7
60% принятых
@Романенко: Вы бы уточнили, что конкретно Вас интересует. Тогда можно было бы сделать пояснения. Нужно разъяснить смысл стандартного определения предела функции в точке, или что-то другое?
Просто прокомментирую определение предела функции (вопроса не понял…). У каждой последовательности есть «хвост», в котором значения величины не выходят за границы промежутка определённого размера. Рассматриваем две такие последовательности: в одной последовательности каждый следующий элемент «ближе» к искомой точке «входной» переменной, чем предыдущий; а другая последовательность образована значениями функции для этих значений «входной» переменной. Соответствующие друг другу размеры промежутков, где заключены все значения величин в «хвостах» последовательностей, — это и есть эпсилоны и дельты.
@abracadabra10, а как величина может выходить за границы промежутка? и что значит :»в анализе неуч?»
@abracadabra10 а, ну ясно,т.е. определение говорит,что если задана послед-ть и она стремится к определенному числу,то она за определенные пределы(промежуток) этого числа не выйдет?
@Романенко: это верно с той оговоркой, что за пределы указанного промежутка последовательность не выйдет, начиная с некоторого достаточно большого номера своего члена. Начальные значения (их всегда конечное число) могут при этом вести себя как угодно.
$%lim_ /x>$%. Одна последовательность — это иксы. Чётко указать один следующий элемент для каждого предыдущего нельзя, но, во всяком случае, если одно число по модулю меньше другого, то оно в последовательности дальше. Вторая последовательность — это игреки. Каждому эпсилону, за границы которого рядом с единицей не должен выходить хвост игреков, соответствует дельта, в границах которой рядом с нулём навсегда остаётся хвост иксов. Какой бы маленький ни был эпсилон, всегда можно выделить такой хвост в последовательности иксов, который отправит значения функции внутрь…
Подумал ещё раз… Эти мои рассуждения — это костыли для «эпохи потенциальной бесконечности»… Если принимать актуальную бесконечность, то всё намного проще получается: никаких «хвостов» и никаких «обещаний». Так что прошу прощения за «философию».
Означает разговор в режиме «студента со студентом». Два непонимающих могут здорово друг другу помочь иногда.
| Главная ≫ Инфотека ≫ Математика ≫ Видео ≫ История языка эпсилон-дельта от Коши до Вейерштрасса // Галина Синкевич |
| Комментарии: 0 |



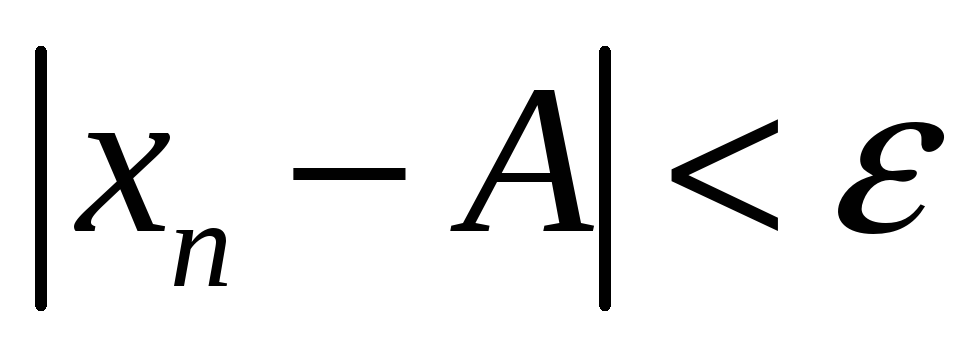
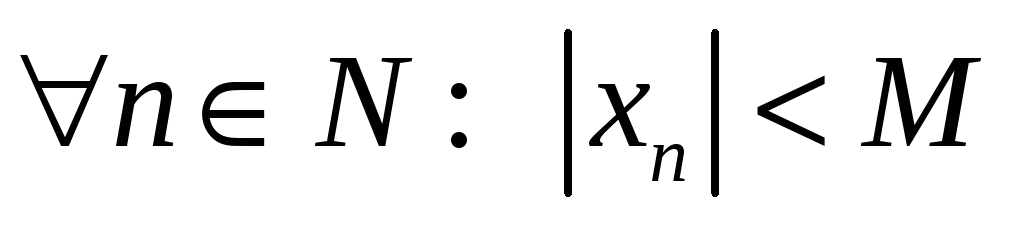
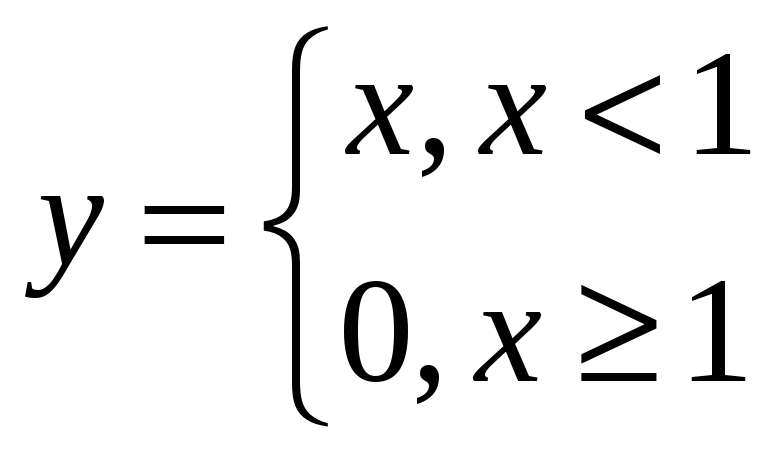
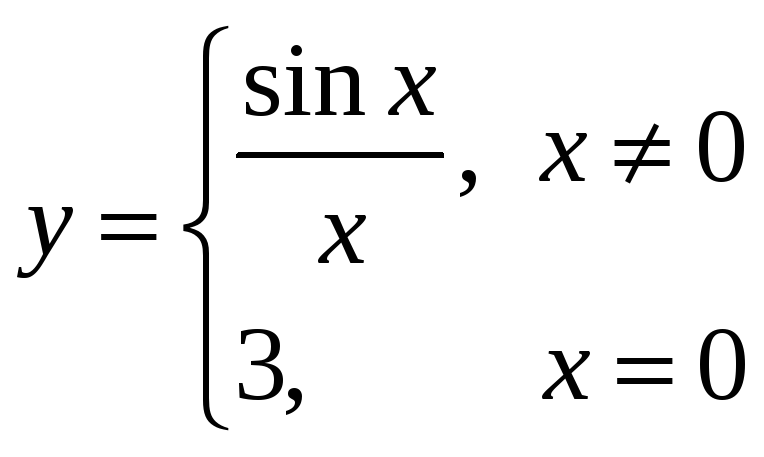
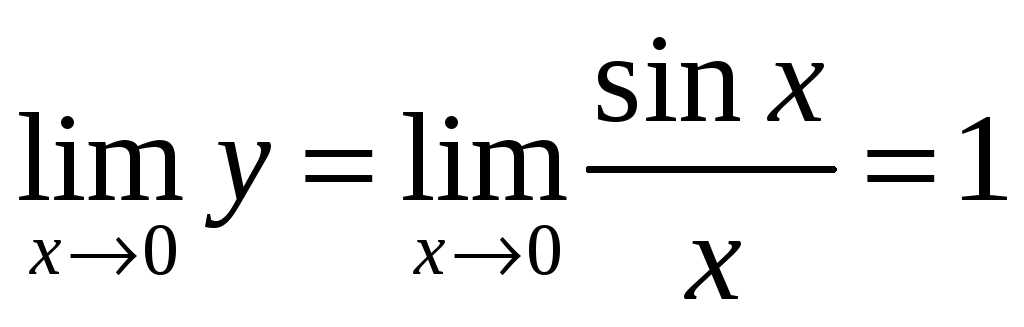
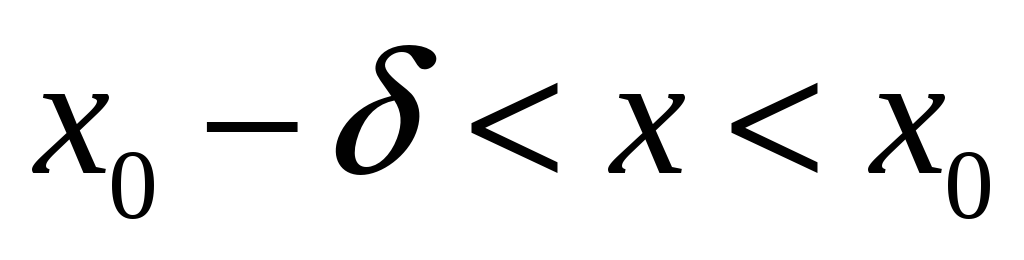
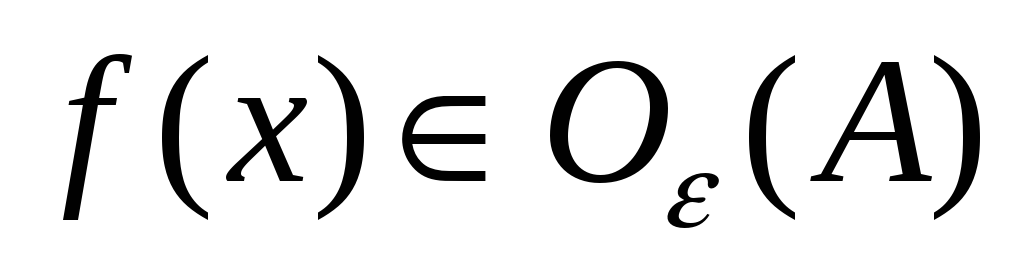
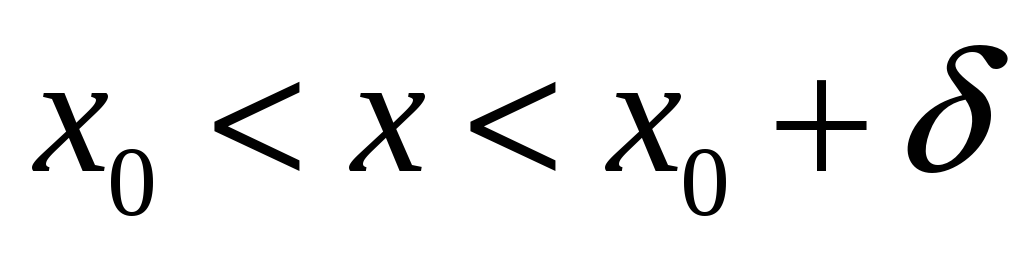
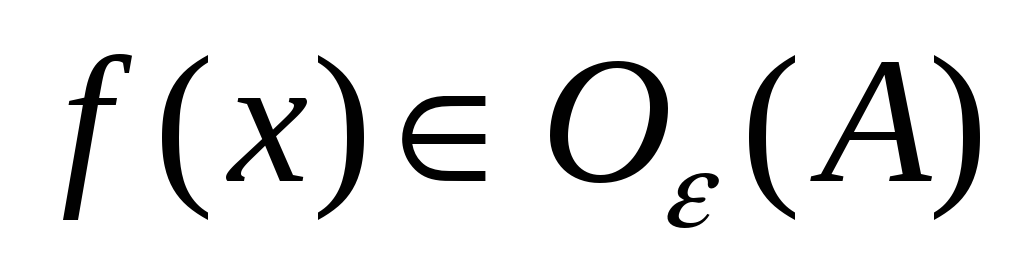

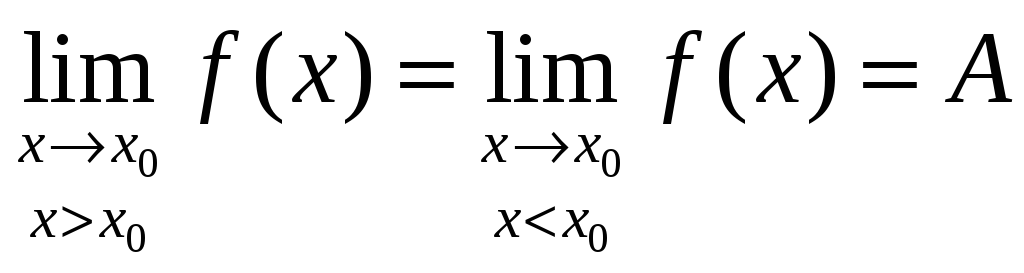
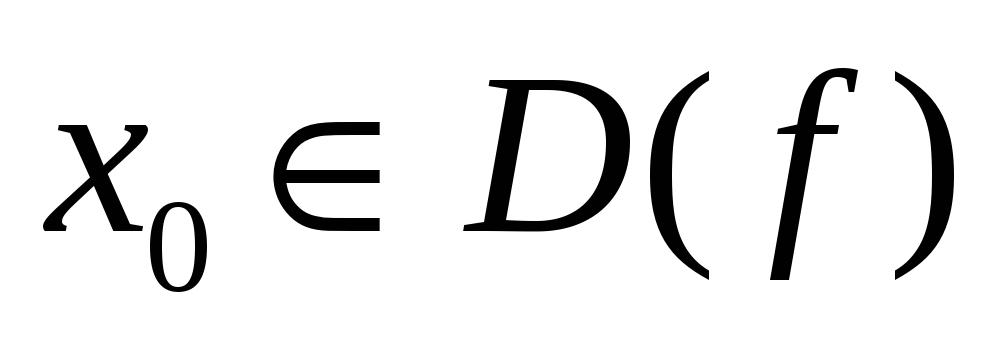
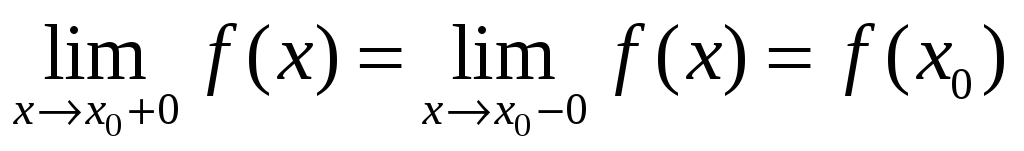
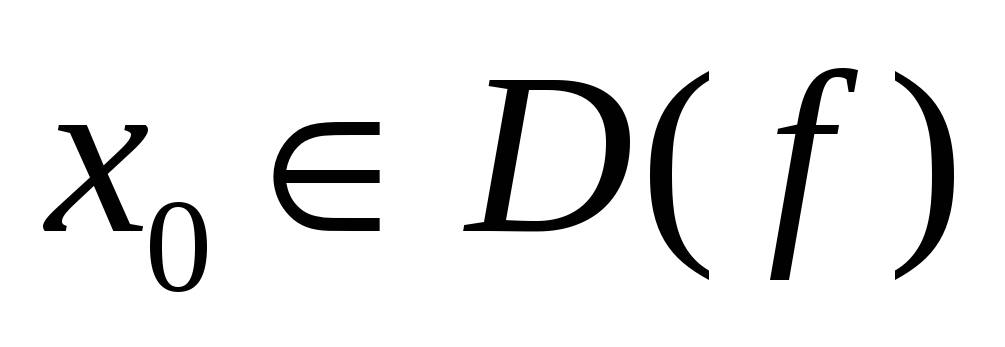
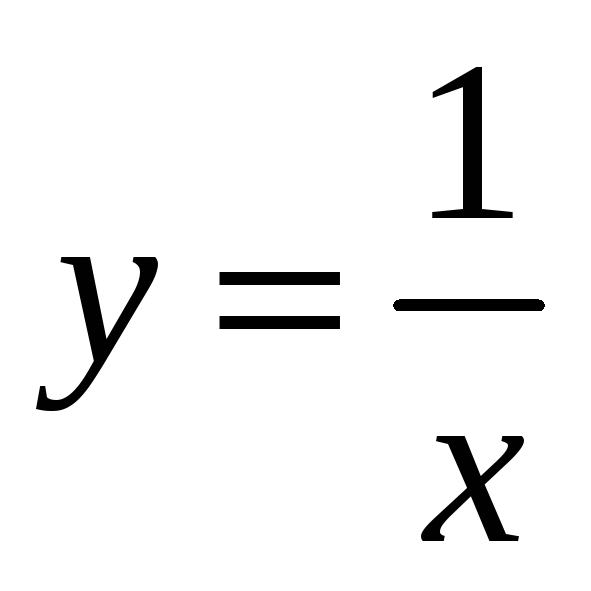
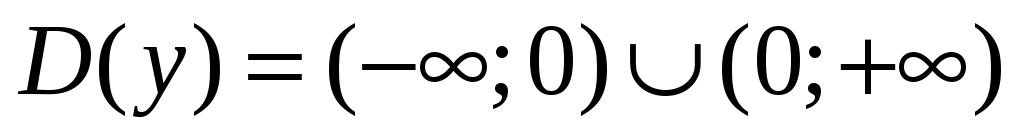
 Язык эпсилон дельта для чайников
Язык эпсилон дельта для чайников
 Язык эпсилон дельта символы
Язык эпсилон дельта символы
![Язык эпсилон дельта для чайников Язык эпсилон дельта для чайников: Использование [ править | править код ]](https://altarena.ru/wp-content/uploads/2021/05/nesmolkaemie_5.jpg) Использование [ править | править код ]
Использование [ править | править код ]

 Ответы к ГОСу / 5
Ответы к ГОСу / 5